Assimilation de données météorologiques
1 ) L'assimilation de données météorologiques : Généralités
2 ) Méthode des moindres carrés
1 ) L'assimilation de données météorologiques : Généralités
La prévision météorologique numérique présente sous forme de modelés météorologiques dépend en grande partie des conditions initiales qui lui sont fournies .
Or, les modèles numériques contiennent 10^7 valeurs correspondant à tous les champs physiques .
Mais les observations ne contiennent que 10^6 valeurs : en effet, les seules données d'observations disponibles à un instant t sont les observations météorologiques issues entre autres de radiosondages, de stations météorologiques professionnelles et de bouées météorologiques .
Du coup, de nombreuses données d'observation arrivent en retard au centre de calcul servant à l'élaboration de l'analyse : ces données sont donc perdues .
Une interpolation simple de toutes les valeurs ( observation + modele ) ne suffit donc pas .
Il faut donc une méthode qui intègre toutes les données d'observations dans la détermination de l'état initial de l'atmosphère et ainsi établir une prévision calculée au pas de temps précédent et donc valable à l'instant donné : c'est la méthode d'assimilation de données météorologiques .
La méthode d'assimilation de données météorologiques est une méthode utilisée dans les modèles numériques de prévision météorologique dans le but de prendre en compte le plus possible de données d'observation pouvant contribuer à décrire l'état initial de l'atmosphère .
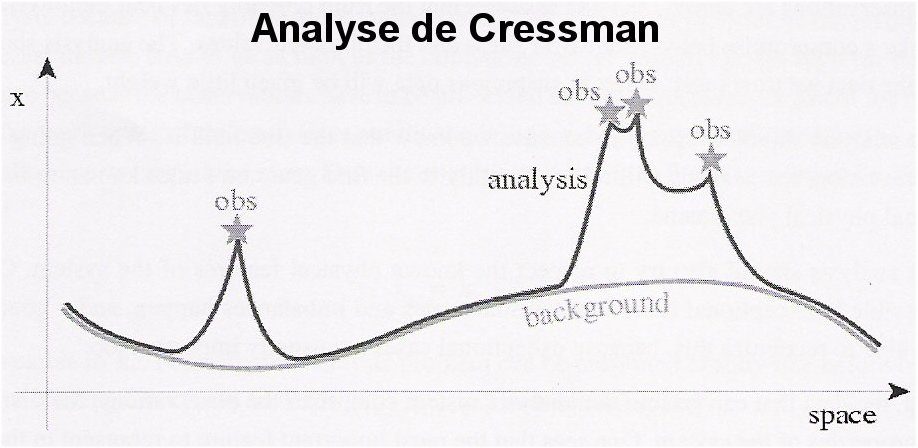
Nous avons sur l'image ci-dessous un exemple d'analyse de Cressman en prenant un champ d'observation à une dimension :

C'est un algorithme dans lequel le modèle est calqué sur les valeurs observées en tenant compte des observations valables et sur un état arbitraire .
Le background est une prévision de l'état du modèle qui est la courbe représentant le paramètre Xb ( champ initial ) en question sans modification des données : la courbe est jolie certes mais il manque l'essentiel des informations notamment certaines observations .
La courbe de couleur noire est l'analyse produite par l'interpolation entre Xb et les valeurs observées ( plus les observations sont proches de Xb, plus elles ont de l'importance ) .
Pour déterminer l'analyse Xa, nous nous servons de la méthode des moindres carrés .
2 ) Méthode des moindres carrés
La méthode des moindres carrés permet de comparer les données expérimentales qui sont le plus souvent entachées d'erreurs de mesures à un modèle météorologique dans le cas qui nous intéresse et qui est censé décrire ces données .
Le modèle météorologique peut prendre diverses formes : la forme que nous voulons qu'il prenne est telle que l'impact des erreurs expérimentales en ajoutant des données d'observations dans le calcul est minimiser .
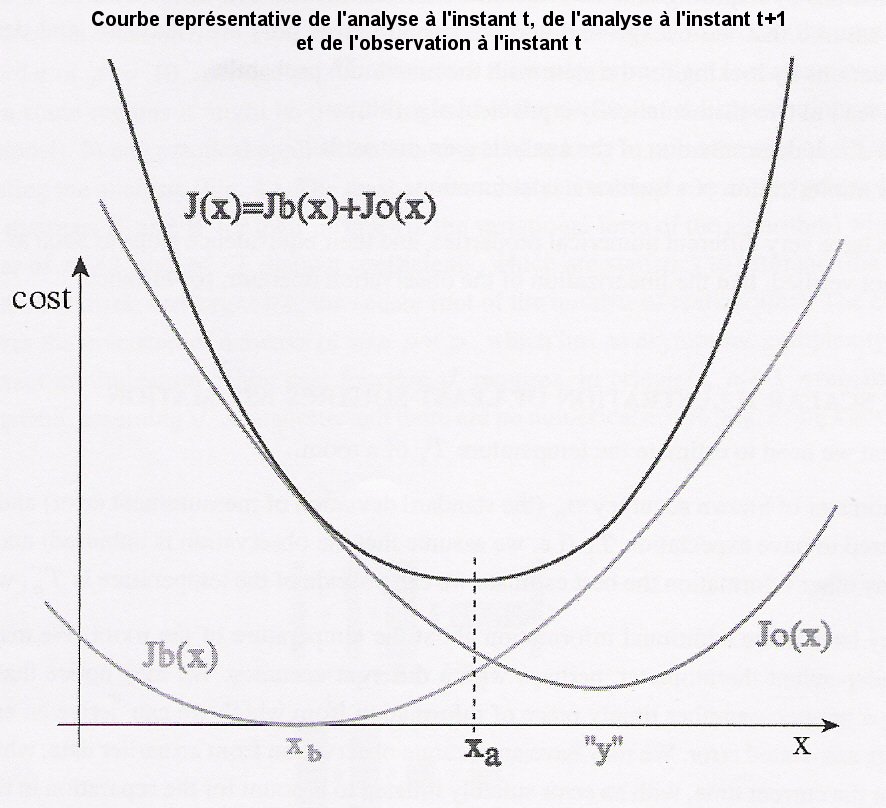
Ici, le modèle météorologique sera une équation de la forme définie sur l'image ci dessus .
Xa : analyse ( champ modifié ) qui est aussi l'estimateur des moindres carrés .
Xb : prévision météorologique .
Y : observations .
K : opérateur linéaire .
H : opérateur d'observation ; il consiste à modifier le champ initial Xb issu de la prévision du modèle météorologique en tenant compte de l'observation Y pour donner le champ modifié Xa .Pour des variables simples ( notée X ) comme la température, l'humidité relative et l'intégrale de la densité de vapeur d'eau, nous avons H(X) = X .
B : matrice de covariance des erreurs du background ( erreur de prévisions ) .
R : matrice des erreurs d'observations .
Considérons la distribution e(b) = Xb - Xt
e(b) : vecteur d'erreurs qui les sépare du vrai état initial .
Xt : vraie valeur du modèle .
B = variance de e(b) .
D'un point de vue statistiques, si nous prenons en compte une petite surface d'un histogramme ( dans le cas des données météorologiques, c'est ce qui nous intéresse car les données d'observations concernent une surface infiniment petite ), la distribution e(b) sera une fonction scalaire d'intégrale égale à 1 .
Comme B est de la forme,

que les valeurs propres sont égales entre elles et que B^T=B, alors B ( matrice positive par définition ) peut être assimilé à un scalaire et donc B = 1 .
H étant égal à l'identité ( H=H^T=1 ), nous avons K=B(B+R)^-1 .
Nous prenons R=0.25 pour avoir une meilleure interpolation des données .
Nous prenons dorénavant un système ( par exemple, le système { salle } ) dans lequel nous avons une source de chaleur de 22°C .
Nous souhaitons connaitre la température dans cette pièce .
La source de chaleur ne fonctionne pas au temps t0 : la température dans la pièce est To = 17°C avec une variance des erreurs de mesures notée s²(o) .
Nous activons la source de chaleur . La prévision consiste à dire qu'il fera 22°C au point d'application de la source et une température Tb = 19°C dans un point A assez éloigné de la source .
Nous sortons de la salle, nous y revenons 3 heures après : le thermomètre placé au point A indique une température Ta = 18°C .
L'assimilation de données météorologiques part de l'idée que cette information corrige la prévision précédente c'est-à-dire en supposant par exemple une décroissance rapide de la température au-delà du point d'application .
D'où
Ta = kTo + ( 1 - k )Tb
s²(a) = ( 1 - k )²s²(b) + k²s²(o)
k : valeur qui minimise la variance d'erreurs d'analyse .
Nous choisissons k compris entre 0 et 1 telle que
k = s²(b) / [s²(b) + s²(o)]
En regardant sur l'annexe 2, nous avons la variance des erreurs d'observation en fonction du paramètre k .
Si k = 0, s(o)>>s(b) et Ta = Tb : l'analyse est équivalente au background .
Si k = 1, s(o)<<s(b) et Ta = To + ( To - Tb ) : l'analyse est équivalente à l'observation .
Si k = 1/2, s(o)=s(b) : l'analyse est la moyenne de To et de Tb .
D'où le programme suivant :
//lecture des matrices de données //
m1=read('AN990917.09.dat',-1,4);
m2=read('AN990917.09_y.dat',-1,1);
m3=read('RS990917.12_y.dat',-1,1);
m4=read('AN990917.09.dat',-1,4);
m5=read('RS990917.12_x.dat',-1,1);
// Nous calculons la transposée des matrices m2, m3 et m5 pour avoir des matrices à une ligne et donc faciliter l'interpolation de données//
Tb=m2';
To=m3';
zo=m5';
B=1; // resultat du calcul de la variance des erreurs de l'ébauche //
R=0.25; // résultat du calcul de la variance des erreurs d'observations //
K=B*(B+R)^(-1);
zb=m1(:,1);
Ttemoin=m4(:,3);
// nous faisons en sorte que les valeurs des zb correspondent aux valeurs des zo//
zi=max(zo(1),zb(1));
zf=min(max(zb),max(zo));
var=find(zb>zi & zb<zf); // valeurs des zb correspondant aux zo //
z=zb(var); // nous gardons que les altitudes de zb utiles //
T=interpln([zo;To],z); // interpolation pour les To soient sur la même grille d'altitudes(z) que les Tb //
Ta=Tb(var)+K*(T-Tb(var));
plot2d(z,Ta,6);
plot2d(z,Ttemoin(var),3);
xtitle('Donnees assimilees de la temperature en fonction de l altitude','altitude (m)','temperature (oC)')
legends(["Ttemoin","Ta"],[3,6]);
//plot2d(zb,Tb,1);
//plot2d(z,Ta,2);
//plot2d(zo,To,3);
//xtitle('Donnees assimilees de la temperature en fonction de l altitude','altitude (m)','temperature (oC)')
//legends(["Temperature prevue","Temperature modifiee","Temperature observee"],[1 2 3])
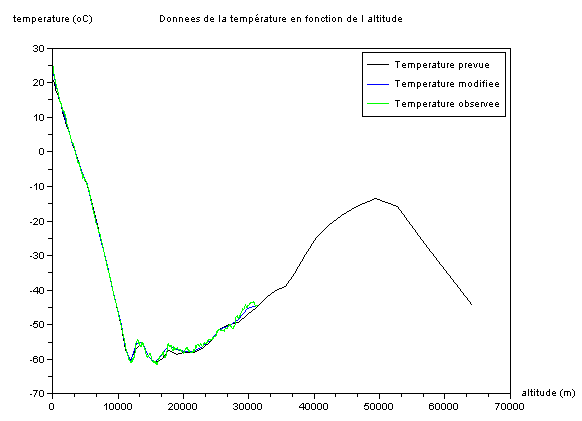
D'où les résultats suivants pour la température :
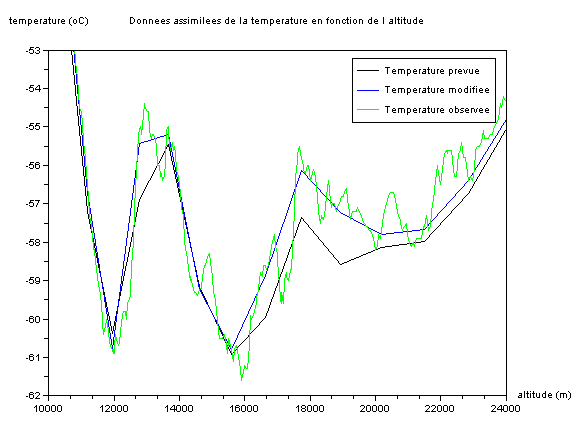
En zoomant :
Les données des fichiers présents dans le programme sont issues du modèle ECMWF ( European Centre for Medium-range Weather Forecasts : Centre Européen de prévisions météorologiques à moyen et long terme c'est à dire de prévisions entre 3 et 6 jours ) avec une fréquence de 3 heures entre les fichiers de données .
Les données datent du 17 Septembre 1999 et se présentent sous la forme de 4 colonnes : altitude (m), pression (hPa), température (°C), humidite relative (%) .
Les fichiers de données d'observations se présentent sous la même forme que les données issues du modèle ECMWF avec une fréquence de 6 heures entre les fichiers de données et un nombre de données nettement plus important, ce qui fait qu'il faut prendre en compte les données utiles .
Les résultats donnent alors des températures en fonction de l'altitude jusqu'à environ 31 km et sont présentés sous la forme suivante :
-les courbes des températures Ta, Tb et To : nous trouvons des graphes ( graphe du haut : représentation globale ; graphe du bas : zoom sur une partie du graphe ) correspondant parfaitement à celui de l'image suivante :
 .
.
-les courbes Ttemoin ( la température que nous devrions avoir ) et Ta ( la température que nous obtenons après interpolation ) : nous voyons très clairement que les données sont fort bien interpolées avec une mention à l'analyse de 12h .
Pour l'humidité relative ( quantité de vapeur d'eau qui se trouve dans une particule d'air / quantité de vapeur d'eau que peut contenir la particule d'air ), nous effectuons la même opération .
Nous pouvons pousser l'étude de l'assimilation de données météorologiques au calcul de l'intégrale de la densité de vapeur d'eau ( notée r(v) ) avec :
r(v) = e / [ R(v)T ]
R(v) = R / MV
e : pression partielle de l'eau .
R(v) : constante spécifique de la vapeur d'eau ( J / K / kg ) .
R : constante des gaz parfaits .
M : masse molaire de l'eau .
Pour représenter les données, il faut effectuer des conversions pour calculer e ( formule de Tetens ) : nous utilisons un fichier convertissant l'humidité en diverses températures dans un programme principal .